|
From 1942-1945/46 (at the same time as he was developing the Z4 computer, as discussed in Part 6 of this article), Konrad Zuse was also developing ideas as to how his machines could be programmed in a very powerful way (that is, more powerful than arithmetic calculations only).
He considered many of the problems that engineers and scientists needed to solve, analyzed and described these problems, and created dozens of examples. Based on these evaluations, it became clear to my father that he required a sophisticated technique for formulating tasks that the computer should solve. For example, one of his ideas was related to performing the calculations used to build bridges. In this case he believed that the input data for a bridge-building program should be the type of bridge required and the conditions of the bridge related to the material and the environment. Based on this, the computer should then propose a reliable bridge.
|
|
|
Zuse denoted such machines as Logistische Maschinen (logistic machines), as opposed to algebraic machines such as the Z1, Z2, Z3 (and the Z4 as described in Part 6), which were only appropriate for numerical calculations. In order to provide this ability to capture the difficult problems of engineers in computer programs, Konrad Zuse formulated the remarkably sophisticated programming language Plankalkül.(4) In addition to pure statements for number calculations, Zuse also used rules of mathematical logic.
|
|
(4)The name Plankalkül is derived as a combination of two words: "Plan" and "Kalkül". Konrad Zuse referred to his programs as a Rechenplans (Computing Plans).
The term Kalkül (calculus) is well known in mathematics, so he put "Plan" and "Kalkül" together to form Plankakül, meaning "calculus for a computing plan".
|
|
|
On the one hand he used the powerful predicate logic Boolean algebra as language constructs. On the other hand he developed a mechanism to define powerful data structures, commencing with the simple bit (binary digit) and working up to complicated hierarchical structures. In order to demonstrate that the Plankalkül language could be used to solve scientific and engineering problems, Konrad Zuse wrote dozens of example programs. In his notes one can find the sorting of lists, search strategies, relations between pairs of lists, etc.
Konrad Zuse focussed on the types of logical problems that have to be solved with the computer. From my point of view there is no other work available (at or before this time) where so many written programs applied to engineering problems can be found. The final version of Plankalkül was finished in Hinterstein (Allgäu) in 1946/46, but it wasnt until 1972 [ZUSE72] that Plankalkül was finally published by the GMD (Gesellschaft für Mathematik und Datenverarbeitung). The reason for such a late publication was the effort Konrad Zuse needed for the Zuse KG company from 1949-1964, as discussed in Part 7 of this article.
|
|
|
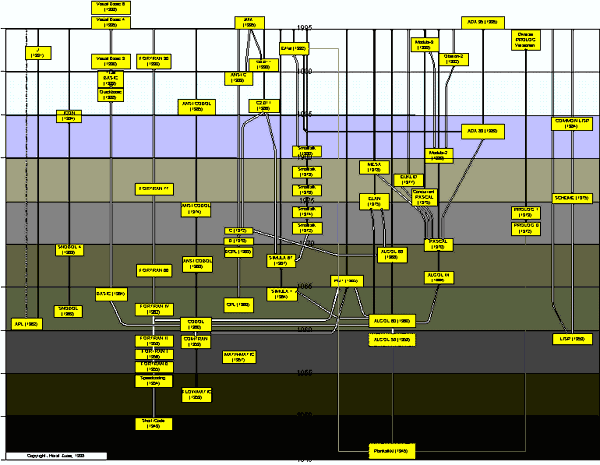
Fig.43a: The history of some important programming languages from 1945 to the present day by Horst Zuse [ZUSE99b]. It is undisputed that Plankalkül was the first programming language for computers in the world. However, the influence of Plankalkül on other languages was minimal.
|
|
| Konrad Zuse used an unusual technique for the statements in Plankalkül. Each data item was denoted with V (variable), C (constant), Z (intermediate result), or R (result), an integer number to mark them, and a powerful notation was used to denote the data structure of the variable. The highlights of Plankalkül are: |
|
|

|
Introduction of the assignment operation, for example: V1 + V2 => R1.
The sign => was introduced by Rutishauser(5) to the ALGOL 60 GAMM-committee, but the committee did not accept it. |
|
|
 |
Statements like V1 = V2 => R1. This means: Compare the variables V1 and V2: If they are identical then assign the value true to R1, otherwise assign the value false. Such operations could also be applied on complicated data structures. |
|
|
 |
Programming plans, calling sub-programs, and different stop criteria. |
|
|
 |
Conditional statements (but no ELSE statement). |
|
|
 |
Repetition of statements (loops). |
|
|
 |
Operations of predicate logic and Boolean algebra. |
|
|
 |
Powerful operations on lists and pairs of lists. |
|
|
 |
No recursion. |
|
|
 |
Data types like: floating point, fixed point, complex numbers. |
|
|
 |
Arrays, records, hierarchical data structures, list of pairs. |
|
|
 |
Arithmetic exception handling. |
|
|
 |
Applications to play chess are described on more than 60 pages. |
|
|
 |
Assertion(6) as was subsequently used in the EIFFEL and MODULA-2 languages. |
|
|
 |
Complicated expressions with parentheses and nesting. |
